川口一晃の「私のテクニカルストラテジー」

第11回ボリンジャーバンド

『偏差値』という言葉を聞くと瞬時に『受験』という言葉を連想してしまうのは、戦後の受験戦争を経験した悲しい性なのかもしれない。偏差値の意味をあまり理解することもなく、受験生を測る一つのモノサシとして、やれ「偏差値70は凄い」、「偏差値50は真ん中」と言って、数字に踊らされていた。実際に社会に出ると、それぞれの人生があの偏差値の数字通りの未来になるわけでは当然ないのだが、当時受験生だった私にとっては、大きなウェイトを持つ数字であることに変りはなかった。
さて、今月は『ボリンジャーバンド』を取り上げる。ボリンジャーバンドは統計学の手法を使ったテクニカル分析で、標準偏差を用いる。マーケットで人気のテクニカル分析の一つだが、筆者はどれだけの投資家がボリンジャーバンドを理解して使っているのかと疑問に思うことがある。もしかしたら、受験生時代のモノサシであった『偏差値』と同様に、意味をよく理解することなくボリンジャーバンドを使っているのではないか、と思うことがあるのだ。そういう意味では偏差値の呪縛がいまだに続いているのかもしれない。今回は、ボリンジャーバンドの数字の意味をしっかりと理解していただきたいと思う。

■標準偏差

ボリンジャーバンドは標準偏差を用いる。標準偏差とは、ひと言で言えば「データのばらつき度合い」をみるものである。

簡単な例を挙げて説明したいと思う。
100人の生徒に対して数学のテストが2回行われたとしよう。1回目および2回目も平均点は50点であった。平均点だけ見れば同じ数字である。しかし、1回目のテストでは、多くの生徒の点数が40点から60点の間に集中していたとする。2回目のテストでは生徒の点数は20点台から80点台まで広く散らばっていた。ここから、2回目の出題範囲に対する理解力に差があったことがわかる。日頃からの勉強の差が出たのが2回目と言えるのかもしれない。

つまり、同じ平均点であっても、その一つ一つのデータの散らばり方を見ることによって、平均値だけからだけでは見えないものが見えてくるということである。

としよう。

この平均点からどれだけ離れているかを表した数値が『偏差』である。

ところが、『偏差』は平均点から離れている数値を表しているものの、プラスの数値もあればマイナスの数値もある。そこで、統計学の手法を用いてプラスやマイナスに関係なく平均値から標準的に離れている数値を表す『標準偏差』を求める。『標準偏差』を言葉で説明するのであれば、『平均値からの標準的な差』となる。そして『標準偏差』を知ることで、それぞれのデータが全体の中でどの位置にいるのかもわかるのである。

例えば、Ａテストの『標準偏差』が10点、Ｂテストのそれが20点であったとする。
Ｂテストの『標準偏差』の数値がＡテストよりも大きいということは、Ｂテストの方が平均値から離れているデータが多く、データのバラつきが大きいことが分かる。

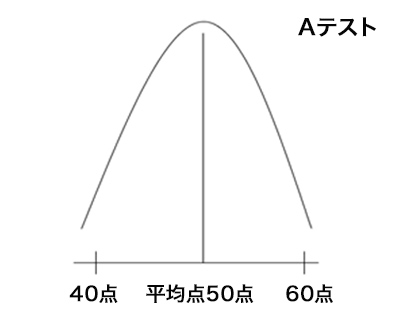
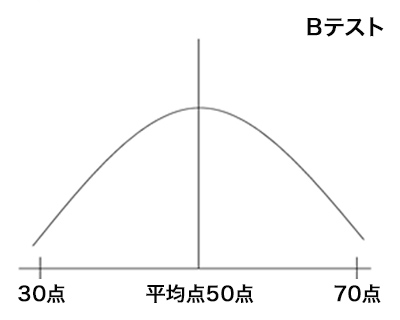
ＡテストおよびＢテストを図にしてみると以下のような図になる。
平均点50点に対してのばらつき度合いがわかる。

そして、ここで是非、覚えていただきたいルールがある。
平均から標準的にプラス方向、マイナス方向に標準偏差一つ分離れている偏差を「1標準偏差」（Aテストでは、40点から60点の間）、二つ分離れている偏差を「2標準偏差」（Ａテストでは、30点から70点の間）と言い、それぞれに以下のようなルールが存在する。
それは平均値から1標準偏差の範囲内に全データの約68％が入り、同じく2標準偏差の範囲内に全データの約95％が入る、というルールである。

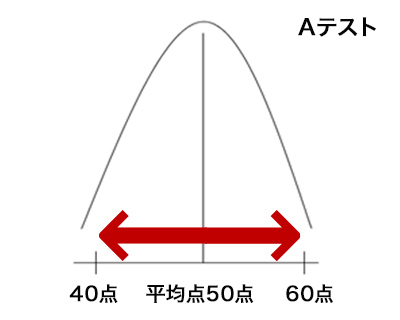
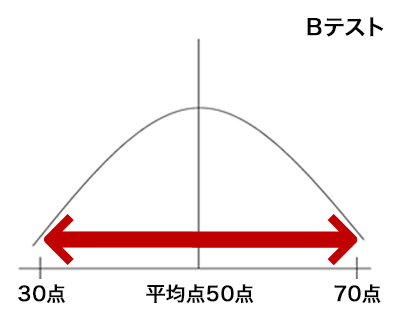
つまり、Ａテストでは40点から60点の間(1標準偏差)におよそ68人の生徒が入る、またＢテストでは30点から70点の間(1標準偏差)に68人の生徒が入る、と考えられるのである。
2標準偏差では、Ａテストは30点から70点の間に、Ｂテストは10点から90点の間に95人の生徒が入ると考えられるのである。

■ボリンジャーバントとは

前章では標準偏差とは何かを学んだ。標準偏差の基本には、『データというものは平均値の周辺に存在している』という考え方がある。

故に、2標準偏差以上に離れた数値というのは、異常値とは言わないが、大変珍しい数値、データということになる。なぜなら5％しか存在しないと考えられるからだ。

では、ここで投資という観点から標準偏差を見ていくことにしよう。
投資で使われる『平均』と言えば、代表的なモノに『移動平均』がある。
単純な移動平均を例に取ると、10日移動平均と言えば、10日間の終値の平均値になる。20日移動平均と言えば、20日間の終値の平均値となる。
この平均値をグラフに表したものが移動平均線であり、トレンドの分析や、マーケットの強弱を判断するのに大変役に立つものである（テクニカルストラテジーの第3回「移動平均線の基本」を参照）。

ここで、移動平均線を確認してみよう。

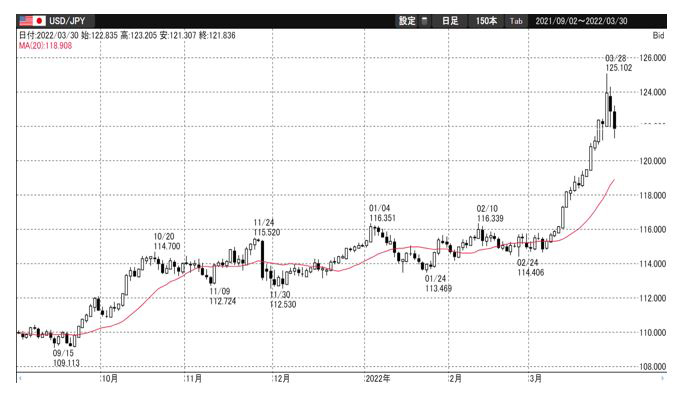
ここでは20日の移動平均線を表示しているが、移動平均線の上下に日々のデータが存在しているのがわかる。つまり、移動平均線を中心にデータがバラついていると見ることができる。
次に、ボリンジャーバンドを使って、移動平均線からのバラツキ度合いを見てみよう。

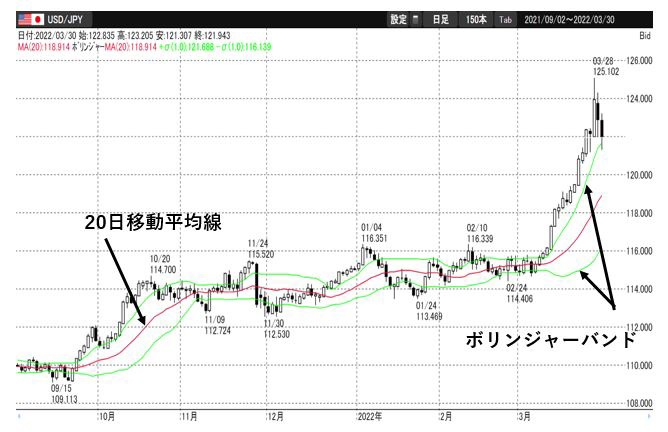
ここでは20日の移動平均に対して±1標準偏差、つまり約68％のデータが入る線、すなわちボリンジャーバンドを描いている。
しかしながら、投資における値動きというのは±1標準偏差を超える場合も多いことから、ボリンジャーバンドを越えて値動きしている場面が多く存在している。

したがって、±1標準偏差ではなく±2標準偏差を使うことを推奨したい。
2標準偏差のボリンジャーバンドを使うと以下のようになる。

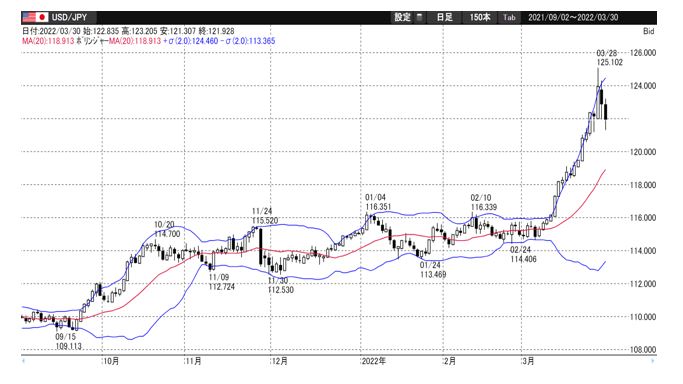
2標準偏差のボリンジャーバンドを描くと、多くの値動きがボリンジャーバンドの内側に存在しているのがわかる。約95％のデータが内側に入ると考えられるからだ。

■ボリンジャーバンドの使い方

ボリンジャーバンドの使い方には大きく2つある。

1. オシレーター系として

   オシレーターというのは、買われ過ぎ・売られ過ぎを分析するテクニカル分析のことである。移動平均線に対して、例えば2標準偏差のボリンジャーバンドを描くことによって、ボリンジャーバンドの外側に出ていく可能性は、上下合わせて5％と考えることができる。つまり、上抜けていくデータはわずか2.5％、割り込んでいくデータも2.5％しか存在しないということになる。であるならば、価格が上下のボリンジャーバンドに到達したのであれば、ボリンジャーバンドを超えていくのではなく、逆の動きになっていく可能性が高いのではないだろうか、と考えるのである。つまり、これは買われ過ぎ・売られ過ぎということになる。

   以下の図を見ていただきたい。

   

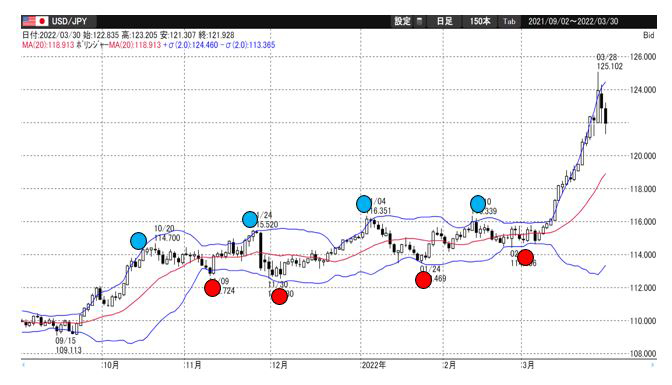
   丸印で示したように2標準偏差のボリンジャーバンドに価格が到達した後に反転しているのがわかる。つまり、売買シグナルを発するポイントでもあると考える。

   この場合は、ボリンジャーバンドをオシレーター系のテクニカル分析として使っているケースである。

2. トレンド系としてのボリンジャーバンド

   以下の図を見ていただきたい。

   

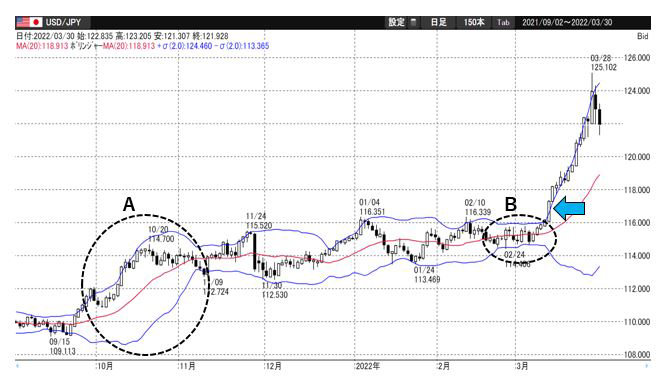
   点線で囲ったAの部分はボリンジャーバンドの幅が広がっているのがわかる。また、B点のそれは逆に狭くなっているのがわかる。

   これは何を意味しているのであろうか。

   Ａの箇所ではバラつきが大きいことを意味している。すなわち、値動きが激しいことを意味している。
   逆に、Ｂの箇所ではバラつきが小さいことを意味している。これは、値動きの小さいもち合いが続いていることになる。
   ところで、値動きの小さなもち合いは、『エネルギーが溜まっている状態』と考える向きが投資の世界では多い。
   故に、ボリンジャーバンドの幅が狭くなった状態の後で2標準偏差を越えていくような大きな値動きが生じた場合には、もち合いを放れ、ブレイクした方向にトレンドが発生したと考え、その値動きに付いていくというのが、ボリンジャーバンドをトレンド系のテクニカル分析として使う場合の考え方である。

■ボリンジャーバンドの活用について

ボリンジャーバンドは人気があるテクニカル分析の一つである。それは冒頭で記したことが影響しているのかもしれない。すなわち、偏差値という数字の中を生きてきた日本人は、この統計学の数字を妙に信じ込んでいる節があるのである。
「2標準偏差の中に95％のデータが入る」と言われれば、オシレーター系のテクニカル分析として重用し、たまに2標準偏差を超える動きが生じると「トレンドが出た」と判断するのだ。
しかし、ここは注意を要する。

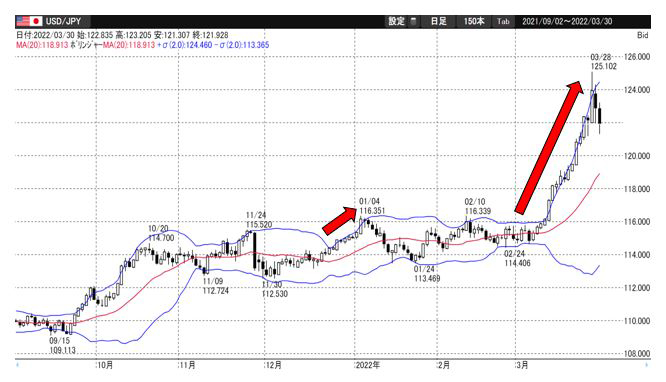
2標準偏差のボリンジャーバンドに到達したとしても、トレンドが出ている場合には翌日もその翌日もボリンジャーバンドとともに推移することが多い。図の矢印の部分である。
この場合、オシレーター系としてボリンジャーバンドを使っていると、毎日が『シグナル点灯』ということになる。つまり、この例で言うと毎日『売りシグナル』が出ることになるのである。

なぜこのようなことが起きるのか。
2標準偏差のボリンジャーバンドの幅というのは、あくまでも昨日ないしは現在までのデータに基づいて計算された数値であり、決して明日の、未来の値幅を示してくれているものではないからだ。私たちが知りたいのは、未来の値動きとその値幅である。
現在までのデータであれば2標準偏差も離れた水準に到達し売りシグナルが点灯しているかもしれないが、明日も上昇すれば2標準偏差離れた水準も更に高くなるのである。

最後は、トレンド系としての使い方の注意点だ。ボリンジャーバンドの幅が小さい時というのはもち合いが続いているということであるから、2標準偏差の数値を越えてきた場合に越えた方向へのトレンドが出現したと判断し追随していく使い方である。
ボリンジャーバンドの幅が厚い、薄いを判断し、ブレイクした方向に付いていくというやり方も理解することはできる。
しかし、見ているチャートのデータ数を増やしたりすると、つまりは期間を延ばしたりすると、それまでに見ていたボリンジャーバンドの幅が小さく見えたりするようになる。つまり、ボリンジャーバンドの幅が狭いか広いかの判断は投資家の主観に委ねられてしまうということなのだ。テクニカル分析を行う際には、なるべく主観を入れる余地を少なくしたい。

ということで、ボリンジャーバンドは人気にあるテクニカル分析ではあるものの、上述したような点を注意しながら分析していく必要があるということを忘れないでいただきたい。